Gradient Flows on Graphons: Existence, Convergence, Continuity Equations

Wasserstein gradient flows on probability measures have found a host of applications in various optimization problems. They typically arise as the continuum limit of exchangeable particle systems evolving by some mean-field interaction involving a gradient-type potential. However, in many problems, such as in multi-layer neural networks, the so-called particles are edge weights on large graphs whose nodes are exchangeable. Such large graphs are known to converge to continuum limits called graphons as their size grows to infinity. We show that the Euclidean gradient flow of a suitable function of the edge weights converges to a novel continuum limit given by a curve on the space of graphons that can be appropriately described as a gradient flow or, more technically, a curve of maximal slope. Several natural functions on graphons, such as homomorphism functions and the scalar entropy, are covered by our setup, and the examples have been worked out in detail.

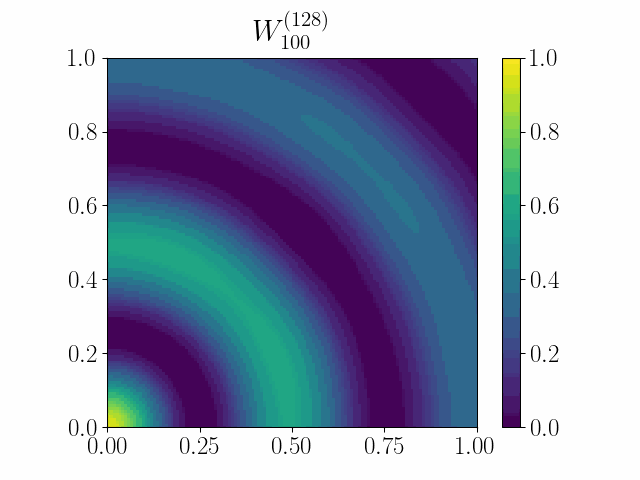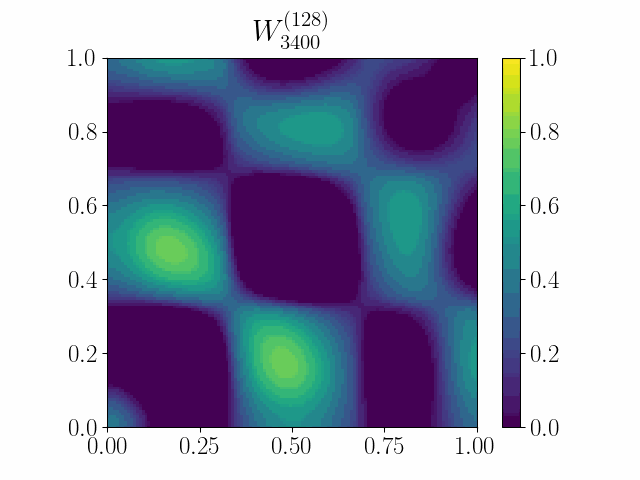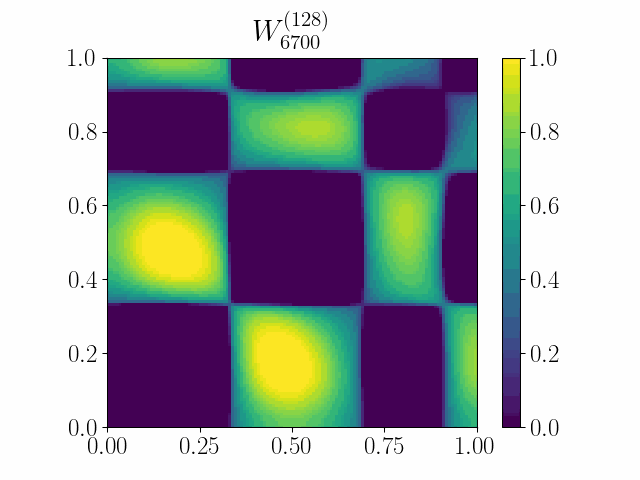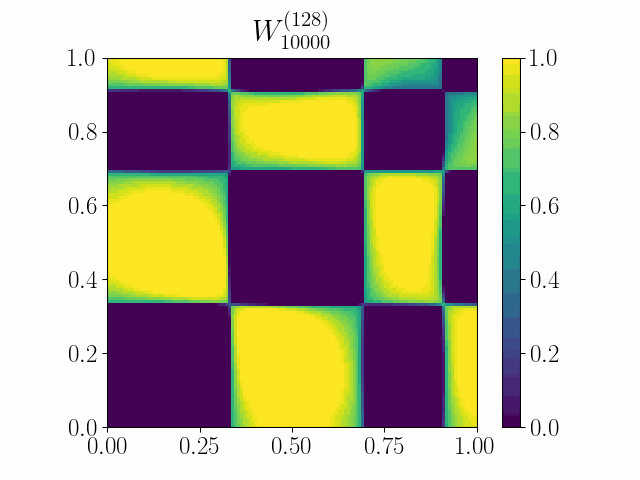
The paper has been accepted at the OTML workshop at NeurIPS 2021. The full version of the paper is acceted at the Journal of Theoretical Probability.

Please find the below resources:

1. OTML poster.
2. Publication.