Scaling laws of optimization algorithms for Deep Learning - the Graphon perspective

Machine Learning models, such as (Deep) Neural Networks ((D)NNs), are growing in size as well as in their efficacy. Gradient-based stochastic optimization algorithms are commonly used to train deep learning models. It is thus important to understand the intricacies of the training dynamics of such large networks. In a simplified model like a two-layer Neural Network (NN), the training dynamics can be considered as a system where each hidden neuron is a “particle” interacting with the others. This concept is often connected to Wasserstein gradient flows, which emerge from these mean-field interactions among exchangeable particles [1,2]. This relies on the observation that the permutation symmetry of the neurons in the hidden layer allows the problem to be viewed as an optimization problem over probability measures.

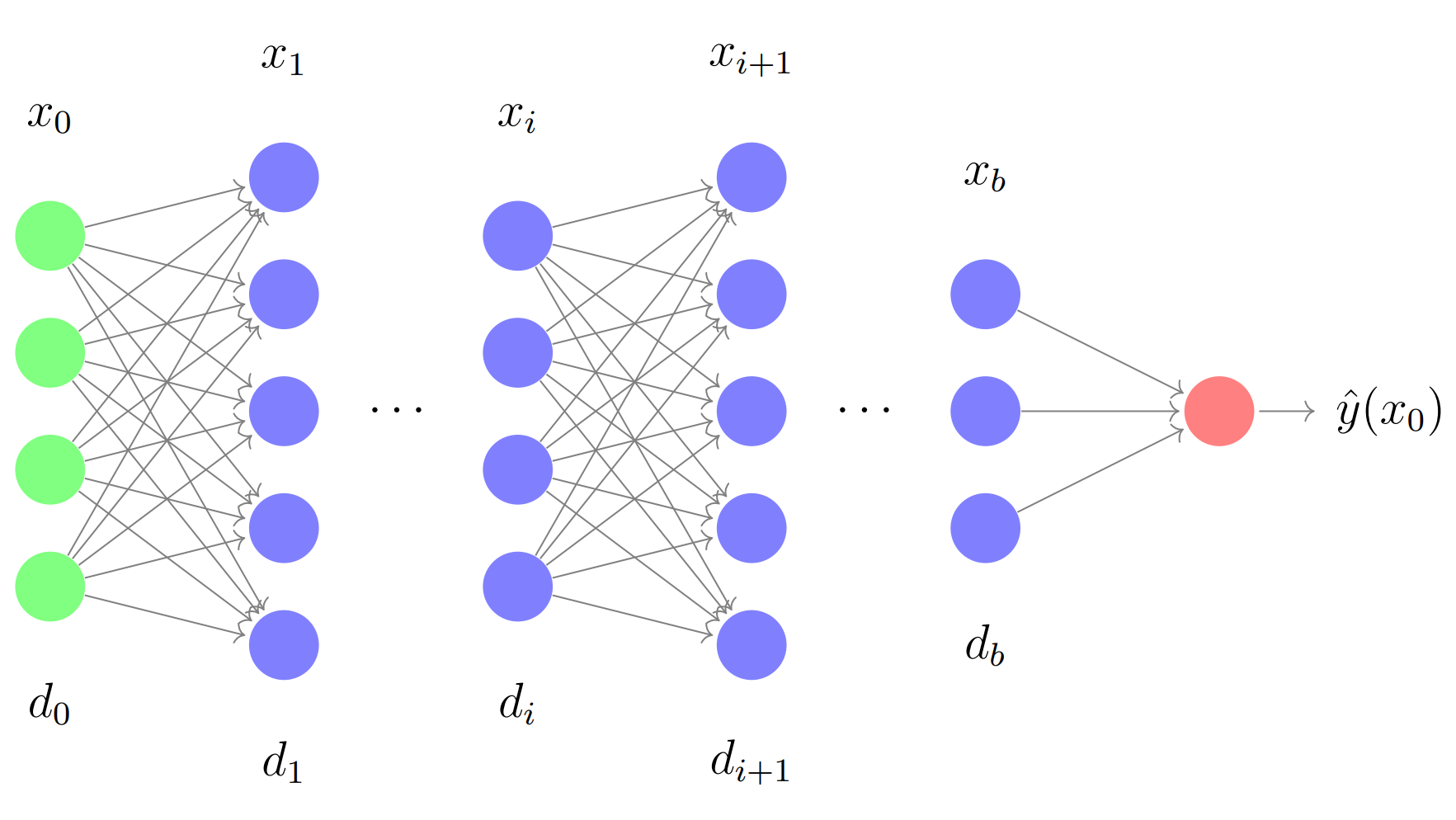
In more complex models, such as multi-layer NNs, that can be considered as large structured computational graphs, these “particles” are the weights of the connections between neurons. The individual neurons in any given layer can be rearranged without changing the output of the network. In such an application, the interacting “particles” are edge weights in a graph whose vertex labels are exchangeable but not the edges themselves. This is a different symmetry at play and restricts the possibility of extension of similar approaches as used earlier [1,2]. Motivated by such optimization problems on graphs, we investigate the question for functions over this class of symmetries.

My recent works show that stochastic optimization algorithms have a well-defined analytical scaling limit as the size of the network grows. The existing theory of graphons (analytical limits of dense unlabeled weighted graphs), and the general theory of gradient flows on metric spaces [3], allow us to characterize a scaling limit of stochastic optimization algorithms as smooth deterministic curves on the space of graphons. We discover a generalized notion of the McKean-Vlasov equations on measure-valued graphons where the phenomenon of propagation of chaos holds. We also analyze a simple zeroth order Meropolis chain MCMC algorithm on (stochastic block models) SBMs on unweighted graphs to sample from a Gibbs measure and show a fascinating link between sampling and optimization. In the asymptotically zero-noise case, the limit of these wide class of algorithms coincide with the gradient flow of the objective function on the metric space of graphons.

Such scaling laws can simplify parameter setting for large experiments and model transfer to new domains. On the theoretical side, scaling laws shed light on empirical phenomena and unify them with mathematical concision.

Publications:

1. Gradient Flows on Graphons: Existence, Convergence, Continuity Equations - Paper, ArXiv.

Research Papers (under review):

1. Path convergence of Markov chains on large graphs - ArXiv.
2. Stochastic optimization on matrices and a graphon McKean-Vlasov limit - ArXiv.

The framework of casting such an optimization problem on graphs as gradient flows on graphons allows us to cast several extremal graph theoretic questions. In the below animation, it is shown that gradient flows can be used to recover Mantel’s theorem. It states that a triangle-free graph with the maximum number of edges is the balanced complete bipartite graph. Here we minimize the difference between the triangle density and the edge density simply by using Euclidean Gradient Descent. The symmetric square adjacency matrix is normalized over the unit square, and we see that the dynamics converges to that of a balanced bipartite graph.

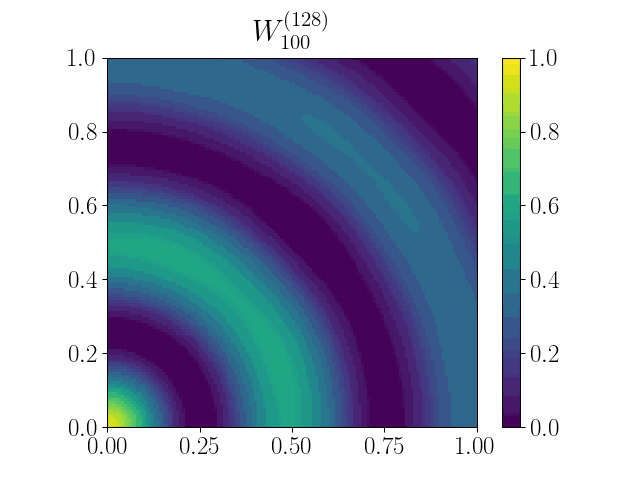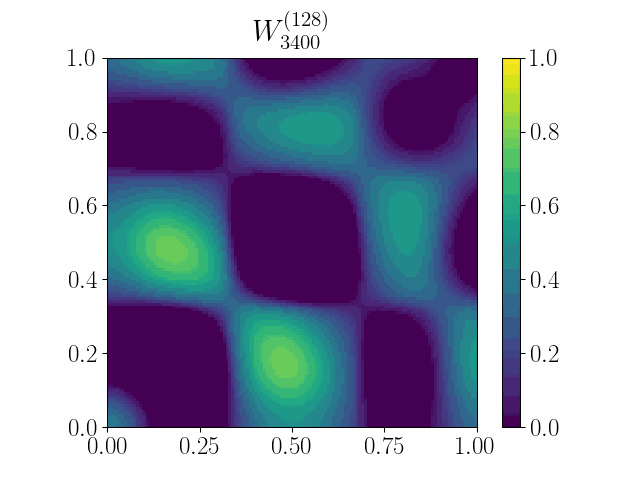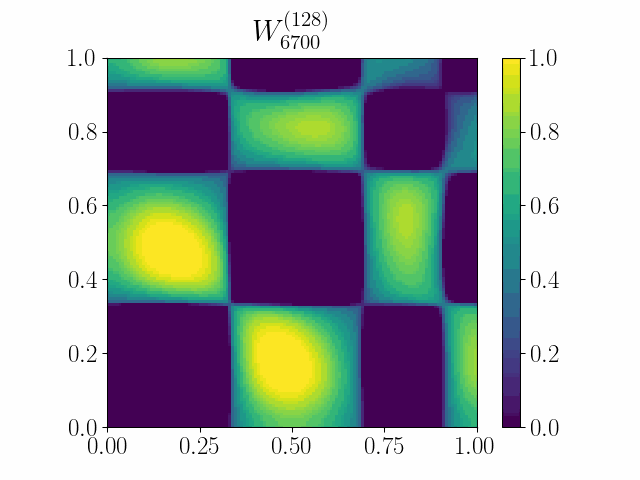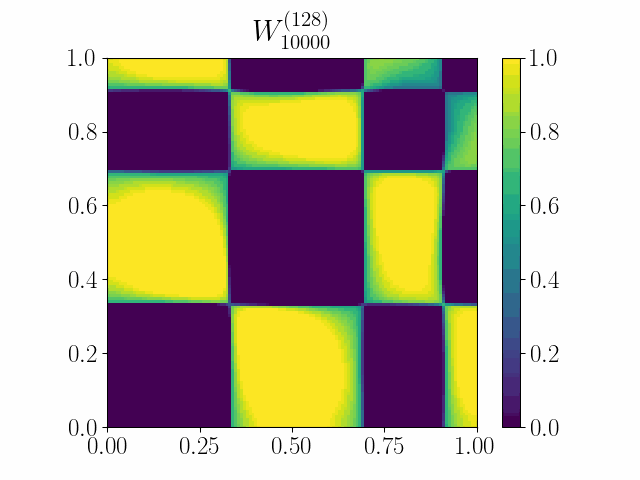
An initial work was accepted at the OTML workshop at NeurIPS 2021.

Our Presentations:

1. OTML workshop at NeurIPS 2021 - poster.
2. The Kantorovich Initiative retreat 2022 - presentation slides.
3. Scaling Laws for Deep Learning Micro-workshop, UW CSE - presentation slides.
4. Machine Learning Foundations seminar, Microsoft Research Redmond - presentation slides.
5. Talk at Applied Optimal Transport workshop at IMSI - presentation video, presentation slides.
6. Talk at UBC PDE + Probability seminar, Pacific Institute for the Mathematical Sciences - Talk.
7. IFML workshop at Simons Institute - poster.
8. IFDS seminar - presentation slides.
9. Poster presentation at Lectures in Probability and Stochastic Processes XV.
10. Google India Research Lab - presentation slides.
11. Talk at the System and Control Engineering department at the Indian Institute of Technology Bombay - presentation slides.
12. Talk at the School of Technology and Computer Science at the Tata Institute of Fundamental Research - presentation slides, YouTube video.
13. Lecture on basics of Graphons at the Department of Computer Science and Engineering at the Indian Institute of Technology Bombay.
14. Talk at the Department of Computer Science and Engineering at the Indian Institute of Technology Bombay - presentation slides.
15. Junior talk at the IFML + KI retreat 2023 - presentation slides.
16. Short talk at IFML workshop 2023 - presentation slides.
17. Probability seminar talk at Brown University.
18. Student prsentation at the Kantorovich Initiative + Scale MoDL retreat 2023 - presentation slides.
19. Generals talk at UW CSE - presentation slides.

References

1. On the Global Convergence of Gradient Descent for Over-parameterized Models using Optimal Transport - Lénaïc Chizat, Francis Bach, 2018.
2. A Mean Field View of the Landscape of Two-Layer Neural Networks - Song Mei, Andrea Montanari, Phan-Minh Nguyen, 2018.
3. Gradient Flows: In Metric Spaces and in the Space of Probability Measures - Luigi Ambrosio, Nicola Gigli, Giuseppe Savaré, 2008.
4. Large networks and graph limits - László Lovász